1.
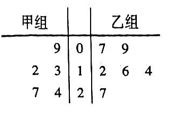
某中学举办了一次知识竞赛,从中随机抽取了部分学生的成绩绘制出如图所示的频率分布直方图,则估计该中学本次竞赛成绩的中位数为( )

A.
68
B.
71
C.
75
D.
79
【考点】
众数、中位数、平均数;