如图所示，已知BD与CE相交于点O，AD=AE，∠B=∠C，请解答下列问题：

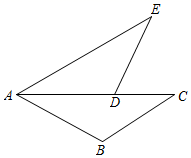
1. 如图所示，已知BD与CE相交于点O，AD=AE，∠B=∠C，请解答下列问题：

(1) △ABD与△ACE全等吗?为什么?

(2) BO与CO相等吗?为什么?

【考点】

三角形全等及其性质; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 将两个三角形纸板 $\text{[math]}$ 和 $\text{[math]}$ 按如图所示的方式摆放，连接DC ．已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 试说明： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

解答题普通

2. 如图所示，已知∠B=90°，△ADC是以CD为底边的等腰直角三角形，过点D作AB的垂线交AB于点E.

(1) 试说明：△ABC≌△DEA；

(2) 若BE=5，CB=4，求DE的长.

解答题普通

3. 已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点C作 $\text{[math]}$ ，垂足为D．在射线 $\text{[math]}$ 上截取 $\text{[math]}$ ，过点E作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点F．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

解答题普通