1.
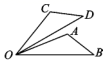
△ABC和△ADC中,下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将两个论断作为条件,另一个论断作为结论构成一个命题,写出一个真命题:.
【考点】
三角形全等的判定-SAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练