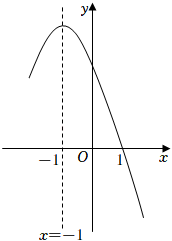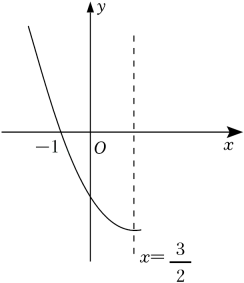
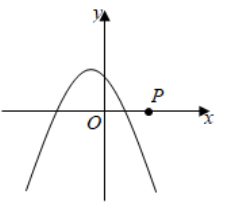
根据解析式业出二次函数图象，并结合图象从开口方向、对称轴、顶点坐标、是否过定点、变化对函数图象的影响几个方面分析图象特征．

1. 根据解析式业出二次函数图象，并结合图象从开口方向、对称轴、顶点坐标、是否过定点、 $\text{[math]}$ 变化对函数图象的影响几个方面分析图象特征．

(1) $\text{[math]}$ ；

(2) $\text{[math]}$ ；

(3) $\text{[math]}$ ；

(4) $\text{[math]}$ ；

(5) $\text{[math]}$ ．

【考点】

二次函数图象与系数的关系; 二次函数y=ax²+bx+c的图象; 二次函数y=ax²+bx+c的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图 W3-2，在平面直角坐标系中，已知线段 $\text{[math]}$ ．

(1) 若抛物线 $\text{[math]}$ 与线段 $\text{[math]}$ 只有一个公共点，结合函数图象，求 $\text{[math]}$ 的取值范围；

(2) 若抛物线 $\text{[math]}$ 与线段 $\text{[math]}$ 只有一个公共点，结合函数图象，求 $\text{[math]}$ 的取值范围．

解答题困难

2. 已知，关于 $\text{[math]}$ 的二次函数 $\text{[math]}$ ．

(1) 若函数 $\text{[math]}$ 经过点 $\text{[math]}$ ，求拋物线的对称轴．

(2) 若点P(t-2，p)，Q(t+3，q)均在抛物钱y=2x²-4tx-3上，则pq(填">"，“<"或"=”).

(3) 记 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 始终成立，求 $\text{[math]}$ 的取值范围．

解答题困难

3. 在平面直角坐标系中，设抛物线 $\text{[math]}$ ，其中 $\text{[math]}$ .

(1) 若抛物线的对称轴为 $\text{[math]}$ ，求抛物线的解析式；

(2) 若 $\text{[math]}$ ，点 $\text{[math]}$ 与点 $\text{[math]}$ 是抛物线上两个不同的点，且 $\text{[math]}$ ，求证： $\text{[math]}$ .

解答题普通