1.
已知 和
和 都是等腰直角三角形,
都是等腰直角三角形,
 的顶点
的顶点 在
在 的斜边
的斜边 上.
上.

(1)
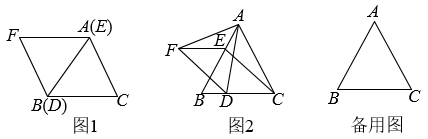
如图1,连接 .
(2)
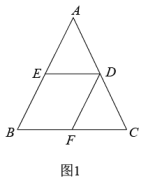
如图2,若
.
(2)
如图2,若 , 点F是
, 点F是 的中点,求
的中点,求 的长.
的长.
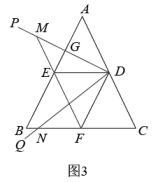
①请你探究与
之间的关系,并证明你的结论;
②求证: .
【考点】
三角形的综合;
能力提升
真题演练