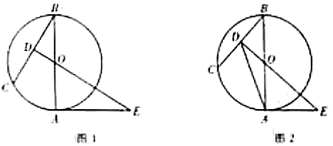
1.
如图,C、D是以AB为直径的⊙O上的点, =
= , 弦CD交AB于点E.
, 弦CD交AB于点E.

(1)
当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)
求证:BC2﹣CE2=CE•DE;
(3)
已知OA=4,E是半径OA的中点,求线段DE的长.
【考点】
勾股定理;
圆的综合题;