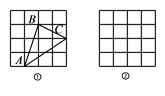1.
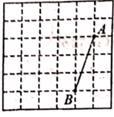
如图是由边长为1的小正方形构成6×6的网格.每个小正方形的顶点叫做格点.线段AB的端点在格点上.点P是AB与网格线的交点,仅用无刻度尺的直尺在给定网格中画图.画图过程用虚线表示、画图结果用实线表示.按步骤完成下列问题:

(1)
直接写出AB的长为 ;
(2)
请以AB为边,在图中画格点正方形ABCD;
(3)
在图中CD边上画点Q , 连接PQ , 使得四边形BCQP的面积为5.
【考点】
勾股定理;
正方形的性质;