1.
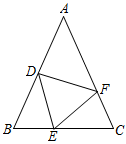
等边三角形ABC与正方形DEFG按如图①所示的方式放置，其中D，E两点分别在AB，BC上，且BD=BE.
(1)
求∠DEB的度数。
(2)
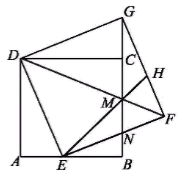
当正方形DEFG沿着射线BC方向以每秒1个单位的速度平移时，CF的长度y随着运动时间t变化的函数图象如图②所示，且当
时，y有最小值1。
①求等边三角形ABC的边长。
②连结CD，在平移的过程中，当△CEF与△CDE同时为等腰三角形时，求t的值。
③从平移运动开始，到GF恰落在AC边上时，请直接写出△CEF外接圆圆心的运动路径的长度。
【考点】
等腰三角形的判定与性质;
等边三角形的判定与性质;
正方形的性质;
平移的性质;
三角形全等的判定-SAS;
