1.
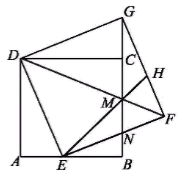
如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.
(1)
求证:CD⊥CG;
(2)
若tan∠MEN=  ,求
,求  的值;
(3)
已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为
的值;
(3)
已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为  ?请说明理由.
?请说明理由.
【考点】
正方形的性质;
能力提升
真题演练