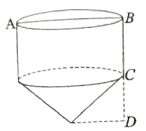
已知圆锥的侧面展开图是一个半径为4的半圆．若用平行于圆锥的底面，且与底面的距离为的平面截圆锥，将此圆锥截成一个小圆锥和一个圆台，则小圆锥和圆台的体积之比为．

1. 已知圆锥的侧面展开图是一个半径为4的半圆．若用平行于圆锥的底面，且与底面的距离为 $\text{[math]}$ 的平面截圆锥，将此圆锥截成一个小圆锥和一个圆台，则小圆锥和圆台的体积之比为．

【考点】

组合几何体的面积、表面积、体积问题; 旋转体（圆柱/圆锥/圆台/球）的结构特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 已知圆台的上底面半径为1，下底面半径为5，侧面积为30π，则圆台的高为.

填空题容易

2. 已知圆台 $\text{[math]}$ 的体积为 $\text{[math]}$ ，其上底面圆 $\text{[math]}$ 半径为1，下底面圆 $\text{[math]}$ 半径为4，则该圆台的母线长为.

填空题容易

3. 若圆锥的侧面展开图是半径为2的半圆，则该圆锥的高为．

填空题容易