1.
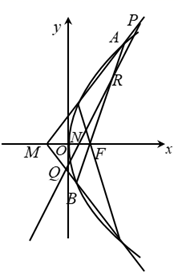
已知过抛物线 的焦点F , 斜率为2的直线交抛物线于A , B两点,且
的焦点F , 斜率为2的直线交抛物线于A , B两点,且 .
.
(1)
求抛物线的方程;
(2)
抛物线的准线与x轴交于点 , 过点
, 过点 的直线l交抛物线于M , N两点,当
的直线l交抛物线于M , N两点,当 时,求直线l的方程.
时,求直线l的方程.
【考点】
抛物线的标准方程;
直线与圆锥曲线的综合问题;
能力提升
真题演练