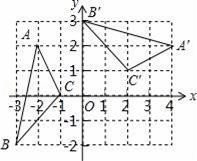
如图，点的坐标为，点的坐标为，点的坐标为，点的坐标为．小明发现线段与线段存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，你认为这个旋转中心的坐标是．

1. 如图， $\text{[math]}$ 点的坐标为 $\text{[math]}$ ， $\text{[math]}$ 点的坐标为 $\text{[math]}$ ， $\text{[math]}$ 点的坐标为 $\text{[math]}$ ， $\text{[math]}$ 点的坐标为 $\text{[math]}$ ．小明发现线段 $\text{[math]}$ 与线段 $\text{[math]}$ 存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，你认为这个旋转中心的坐标是．

【考点】

旋转对称图形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 如图，该图形绕着点O旋转能与自身完全重合，则旋转角最小为 °．

填空题容易

2. 国旗上的每一个五角星是旋转对称图形，它至少需要旋转°后才能与自身重合．

填空题容易

3. 如图，该图形绕其中心旋转能与其自身完全重合，则其旋转角最小为度．

填空题容易