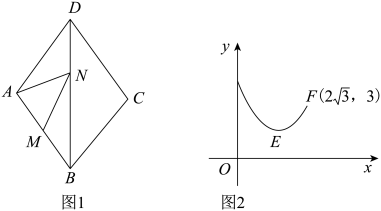
某班级在探究“将军饮马问题”时抽象出数学模型：直线同旁有两个定点A、B，在直线上存在点，使得的值最小.解法：如图1，作点关于直线的对称点，连接，则与直线的交点即为，且的最小值为.请利用上述模型解决下列问题：

1. 某班级在探究“将军饮马问题”时抽象出数学模型：

直线 $\text{[math]}$ 同旁有两个定点A、B，在直线 $\text{[math]}$ 上存在点 $\text{[math]}$ ，使得 $\text{[math]}$ 的值最小.解法：如图1，作点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 与直线 $\text{[math]}$ 的交点即为 $\text{[math]}$ ，且 $\text{[math]}$ 的最小值为 $\text{[math]}$ .请利用上述模型解决下列问题：

(1) 几何应用：如图2， $\text{[math]}$ 中， $\text{[math]}$ 是AB的中点， $\text{[math]}$ 是BC边上的一动点，则 $\text{[math]}$ 的最小值为；

(2) 几何拓展：如图3， $\text{[math]}$ 中， $\text{[math]}$ ，若在AB上取一点 $\text{[math]}$ ，则 $\text{[math]}$ 的值最小值是.

【考点】

等边三角形的判定与性质; 勾股定理; 轴对称的应用-最短距离问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题困难

1. 如图，已知 $\text{[math]}$ ， P是 $\text{[math]}$ 内一点， $\text{[math]}$ ， M、N分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的动点，则 $\text{[math]}$ 的周长的最小值是．

填空题普通

2. 如图， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 的角平分线上， $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 是 $\text{[math]}$ 两边 $\text{[math]}$ 、 $\text{[math]}$ 上的动点，当 $\text{[math]}$ 的周长最小时，点 $\text{[math]}$ 到 $\text{[math]}$ 距离是.

填空题普通

3. 如图，已知直线AB与y轴交于点A（0，2），与x轴的负半轴交于点B，且∠ABO＝30°，点C为x轴的正半轴上一点，将线段CA绕点C按顺时针方向旋转60°得线段CD，连接BD，若BD＝ $\text{[math]}$ ，则点C的坐标为．

填空题普通