1.
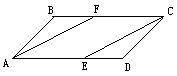
如图,在△ABC的边BC的同侧分别作等边三角形ABD,BCF和ACE.

(1)
证明:△ABC≌△DBF.
(2)
证明:四边形AEFD是平行四边形.
(3)
若AB=3,AC=4,BC=5,则∠DFE的度数为°.
【考点】
等边三角形的性质;
勾股定理的逆定理;
平行四边形的判定;
圆周角定理;
三角形全等的判定-SAS;
能力提升