1.
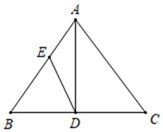
如图,在△ABD中,BA=BD,在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=n°,求∠DAC的度数(用含n的代数式表示).

【考点】
三角形内角和定理;
三角形的外角性质;
等腰三角形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练