1.
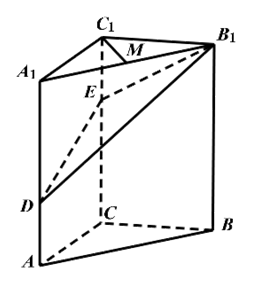
在三棱柱 中,侧面正方形
中,侧面正方形 的中心为点
的中心为点 ,
,  平面
平面 , 且
, 且 ,
,  , 点
, 点 满足
满足 (
( ).
).

(1)
求直线 与平面
与平面 的夹角正弦值;
(2)
若平面
的夹角正弦值;
(2)
若平面 与平面
与平面 的夹角的余弦值为
的夹角的余弦值为 , 求
, 求 的值.
的值.
【考点】
用空间向量研究直线与平面所成的角;
用空间向量研究二面角;