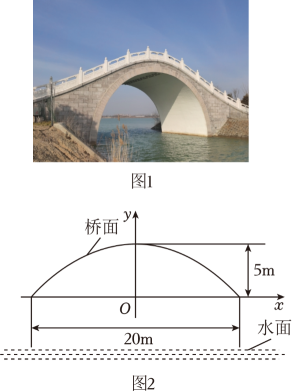
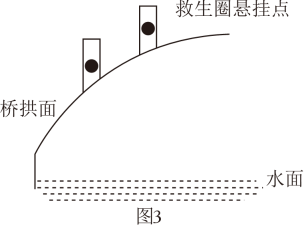
【综合与实践】根据以下素材，探索完成任务．素材1 图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽，拱顶离水面．据调查，该河段水位在此基础上再涨达到最高．素材2 为迎佳节，拟在图1桥洞前面的桥拱上悬挂长的灯笼，如图3．为了安全，灯笼底部距离水面不小于；为了实效，相邻两盏灯笼悬挂点的水平间距均为；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．

1. 【综合与实践】根据以下素材，探索完成任务．

素材1 图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽 $\text{[math]}$ ，拱顶离水面 $\text{[math]}$ ．据调查，该河段水位在此基础上再涨 $\text{[math]}$ 达到最高．

素材2 为迎佳节，拟在图1桥洞前面的桥拱上悬挂 $\text{[math]}$ 长的灯笼，如图3．为了安全，灯笼底部距离水面不小于 $\text{[math]}$ ；为了实效，相邻两盏灯笼悬挂点的水平间距均为 $\text{[math]}$ ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．

(1) 任务1 确定桥拱形状：在图2中建立合适的直角坐标系，求抛物线的函数表达式．

(2) 任务2 探究悬挂范围：在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．

(3) 任务3 拟定设计方案：请你设计一种符合所有悬挂条件的方案．

【考点】

二次函数的实际应用-拱桥问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 请阅读信息，并解决问题：

问题	琴桥检修后需要更换吊杆及相关装饰品
查询信息	宁波有许多桥，有一座横跨鄞州和海曙的桥，因其外形酷似竖琴称为“琴桥”．琴桥的桥拱固定在桥面上，拱的两侧安装了17对吊杆（俗称“琴弦”）.琴桥全长120米，拱高25米.
处理信息	如图是琴桥的主视图，A，B 分别表示是桥的起点和终点，桥拱可看成抛物线，拱的两端 C，D 位于线段 AB 上，且 AC=BD.一根琴弦固定在拱的对称轴 OH 处，其余 16 根琴弦对称固定在 OH 两侧，每侧各 8 根．记离拱端 C 最近的一根为第 1 根，从左往右，依次记为第 2 根，第 3 根，…OH 为第 9 根，…
测量数据	测得上桥起点 A 与拱端 C 水平距离为 20 米，最靠近拱端 C 的“琴弦”EF 高 9 米，EF 与 OH 之间设置 7 根“琴弦”，各琴弦的水平距离相等，记为 m 米.
解决问题	任务 1：以点H为坐标原点，AB所在的直线为x轴，建立平面直角坐标系，求抛物线的解析式；
	任务 2：求琴弦 EF 与拱端 C 的水平距离 CE 及 m 的值．
	任务 3：若需要在琴弦 EF 与 OH 之间垂直安装一个如左图所示高为 17m 的高音谱号艺术品，艺术品底部在桥面 AB 上，顶部恰好扣在拱桥上边缘，问该艺术品顶部应该安装在哪两根琴弦之间？

实践探究题普通

2. 根据以下素材，探索完成任务．

如何设计拱桥上救生圈的悬挂方案？
素材1	图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，过抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，某时测得水面宽20m ，拱顶离水面最大距离为10m ，抛物线拱形最高点与x轴的距离为5m ．据调查，该河段水位在此基础上再涨1m达到最高．
素材2	为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m，且相邻两救生圈悬挂点的水平间距为4m.为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）

问题解决：

(1) 任务1：确定桥拱形状

根据图2，求抛物线的函数表达式．

(2) 任务2：拟定设计方案

求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．

(3) 任务3：探究救生绳长度

当水位达到最高时，上游一个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数．）

实践探究题普通

3. 根据素材解决问题．

设计货船通过圆形拱桥的方案
素材1	图1中有一座圆拱石桥，图2是其圆形桥拱的示意图，测得水面宽AB＝16m ，拱顶离水面的距离CD＝4m ．
素材2	如图3，一艘货船露出水面部分的横截面为矩形EFGH ，测得EF＝3m ， EH＝10m ．因水深足够，货船可以根据需要运载货物．据调查，船身下降的高度y（米）与货船增加的载重量x（吨）满足函数关系式 $\text{[math]}$ ．

问题解决

(1) 任务1：确定桥拱半径

求圆形桥拱的半径

(2) 任务2：拟定设计方案

根据图3状态，货船能否通过圆形拱桥？若能，最多还能卸载多少吨货物？若不能，至少要增加多少吨货物才能通过？

实践探究题普通