1.
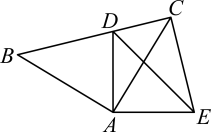
已知△ABC与△CDE都是等腰直角三角形,∠ACB=90°,∠DCE=90°,连接BE , AD , 相交于点F . 求证:

(1)
AD=BE;
(2)
AD⊥BE .
【考点】
等腰直角三角形;
三角形全等的判定-SAS;