1.
某综合与实践小组想要测量如图1所示的池塘 两个端点的距离,但没有足够长的测量工具,两个小组的同学想到了不同的测量方案.
两个端点的距离,但没有足够长的测量工具,两个小组的同学想到了不同的测量方案.

(1)
勤奋小组的同学根据平时学习到的知识,设计了如下的测量方案:
(2)
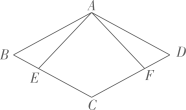
创新小组的同学受到启发,经过组内成员的探究,画出如图2所示的示意图,并得到了如下的测量方案:
①先在池塘一侧的平地上取一个可以直接到达两点的点
(可以测得
的距离);
②连结并延长至点
, 使 ▲ , 连结
并延长至点
, 使 ▲ ;
③连结并测量出它的长度,则 ▲ 的长度就是
两个端点的距离;
④用直尺和圆规在图1中画出测量示意图(不写作法,保留作图痕迹,标明字母);
⑤成员任务分配与实地测量(略).
请你帮勤奋小组的同学将测量方案补充完整,并说明此测量方案合理的理由.
①派一名同学戴一顶太阳帽 , 在点
处立正站好;
②调整太阳帽,使视线通过帽檐正好落在池塘对面的点处;
③该同学旋转后保持方才的姿势,再次使视线通过帽檐,且将视线所落在平地上的位置记为点
;
④测得的长度就是
两个端点的距离.
试说明该测量方案可行的理由.
【考点】
三角形全等及其性质;
三角形全等的判定-SAS;
三角形全等的判定-ASA;