组卷在线网-ZUJUAN.COM

1.

(1) 【问题发现】

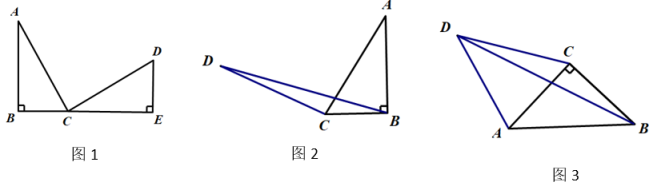
如图1，在△ABC与△CDE中，∠B=∠E=∠ACD＝90°，AC＝CD，B、C、E三点在同一直线上，AB＝4，ED＝3，则BE=.

(2) 【问题提出】

如图2，在Rt△ABC中，∠ABC＝90°，BC＝3，过点C作CD⊥AC，且CD＝AC，求△BCD的面积.

(3) 【问题解决】

如图3，四边形ABCD中，∠ABC=∠CAB=∠ADC＝45°，△ACD面积为14且CD的长为7，求△BCD的面积.

【考点】

余角、补角及其性质; 垂线的概念; 三角形的面积; 等腰直角三角形; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 阅读与理解：

三角形的中线的性质：三角形的中线等分三角形的面积，即如图1，AD是△ABC中BC边上的中线，则S_△_ABD=S_△_AC_D= $\text{[math]}$ S_△AB_C ．

操作与探索：

在图2至图4中，△ABC的面积为a．

(1) 如图2，延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S₁ ，则S₁=．（用含a的代数式表示）．

(2) 如图3，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S₂ ，则S₂=（用含a的代数式表示）．

(3) 在图3的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图4）．若图4中△DEF的面积为S₃ ，则S₃=（用含a的代数式表示）．

实践探究题普通

2. 阅读下面资料：小明遇到这样一个问题：如图 $\text{[math]}$ ，对面积为 $\text{[math]}$ 的 $\text{[math]}$ 逐次进行以下操作：分别延长 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 至 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，使得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，顺次连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，得到 $\text{[math]}$ ，记其面积为 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

小明是这样思考和解决这个问题的：如图 $\text{[math]}$ ，连接 $\text{[math]}$ C、 $\text{[math]}$ A、 $\text{[math]}$ ，因为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，根据等高两三角形的面积比等于底之比，所以 $\text{[math]}$ ，由此继续推理，从而解决了这个问题．

(1) 直接写出 $\text{[math]}$ $\text{[math]}$ 用含字母 $\text{[math]}$ 的式子表示 $\text{[math]}$ ．

(2) 请参考小明同学思考问题的方法，解决下列问题：

如图 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 并延长分别交边 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，则把 $\text{[math]}$ 分成六个小三角形，其中四个小三角形面积已在图上标明，求 $\text{[math]}$ 的面积．

(3) 如图 $\text{[math]}$ ，若点 $\text{[math]}$ 为 $\text{[math]}$ 的边 $\text{[math]}$ 上的中线 $\text{[math]}$ 的中点，求 $\text{[math]}$ 与 $\text{[math]}$ 的比值．

实践探究题普通