1.
已知:点 是等腰直角三角形
是等腰直角三角形 斜边
斜边 所在直线上一点(不与点
所在直线上一点(不与点 重合),连接
重合),连接 .
.

(1)
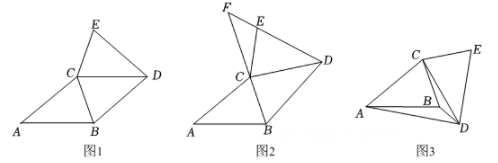
如图1,当点 在线段
在线段 上时,将线段
上时,将线段 绕点
绕点 逆时针方向旋转
逆时针方向旋转 得到线段
得到线段 , 连接
, 连接 .写出
.写出 和
和 的关系并说明理由.
(2)
如图2,当点
的关系并说明理由.
(2)
如图2,当点 在线段
在线段 延长线上时,将线段
延长线上时,将线段 绕点
绕点 逆时针方向旋转
逆时针方向旋转 得到线段
得到线段 , 连接
, 连接 , 画出图形.(1)的结论还成立吗?若成立,请证明;若不成立,说明理由.
, 画出图形.(1)的结论还成立吗?若成立,请证明;若不成立,说明理由.
【考点】
旋转的性质;
三角形全等的判定-SAS;