1.
折叠问题是我们常见的数学问题,它是利用图形变化的轴对称性质解决的相关问题.数学活动课上,同学们以“矩形的折叠”为主题开展了数学活动.
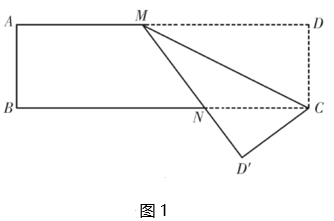
【操作】如图1,在矩形中,点M在边
上,将矩形纸片
沿
所在的直线折叠,使点D落在点
处,
与
交于点N.
【猜想】
(1)
【验证】请将下列证明过程补充完整:
(2)
【应用】
∵矩形纸片沿
所在的直线折叠
∴ ▲
∵四边形是矩形
∴(矩形的对边平行)
∴ ▲ ( )
∴ ▲ ▲ (等量代换)
∴( )
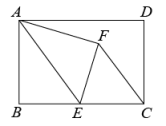
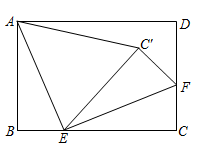
如图2,继续将矩形纸片折叠,使
恰好落在直线
上,点A落在点
处,点B落在点
处,折痕为
.

①猜想与
的数量关系,并说明理由;
②若 ,
, 求
的长.
【考点】
等腰三角形的性质;
勾股定理;
矩形的性质;
翻折变换(折叠问题);
能力提升
真题演练