1.
已知二次函数 与一次函数
与一次函数 .
.
(1)
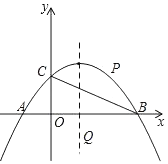
在给出的平面直角坐标系中画出这两个函数的图象.
 (2)
结合图象:
(2)
结合图象:
 直接写出这两个函数图象的交点坐标;
直接写出这两个函数图象的交点坐标;
 直接写出
直接写出 对应的自变量
对应的自变量 的取值范围.
的取值范围.

【考点】
二次函数与一次函数的综合应用;