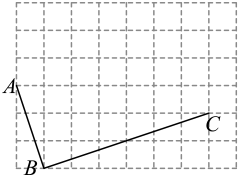
如图是由边长为1的小正方形组成的网格，每个小正方形的顶点称为格点，已知图中A，B，C三点都是格点，且，，．

1. 如图是由边长为1的小正方形组成的网格，每个小正方形的顶点称为格点，已知图中A，B，C三点都是格点，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 请在图中画出平面直角坐标系，并直接写出点B的坐标；

(2) P为格点，若三角形 $\text{[math]}$ 的面积为6，则P点的坐标；

(3) 将线段 $\text{[math]}$ 平移至 $\text{[math]}$ ，使点B与点C重合．

①画出线段 $\text{[math]}$ ， E为线段 $\text{[math]}$ 上一动点，则三角形 $\text{[math]}$ 的面积为 ▲ ；

②若M为 $\text{[math]}$ 上一点，N为 $\text{[math]}$ 上一点，O为坐标原点，当 $\text{[math]}$ 的值最小时，请仅用无刻度的直尺画出点M与点N（保留作图痕迹）．

【考点】

坐标与图形性质; 垂线段最短及其应用; 三角形的面积; 作图﹣平移;

【答案】

您现在未登录，无法查看试题答案与解析。登录

作图题困难

作图题普通

①点 A 与点 B（1，3）的“直角距离”d_AB＝；

②若点 A 与整点 C（﹣2，m）的“直角距离”d_AC＝8，则 m 的值为；

①若对于火警高危点 D 和 E，消防站 P 不仅要满足上述条件，还需要消防站 P 到 D，E

两个点的“直角距离”之差的绝对值最小，则满足条件消防站 P 的坐标可以是（写出一个即可），所有满足条件的消防站 P 的位置共有个；

②在设计过程中，如果社区还有一个火警高危点 F（4，﹣2），那么满足与这三个火警高危点的“直角距离”之和最小的消防站 P 的坐标为．

作图题困难

作图题普通