组卷在线网-ZUJUAN.COM

1.

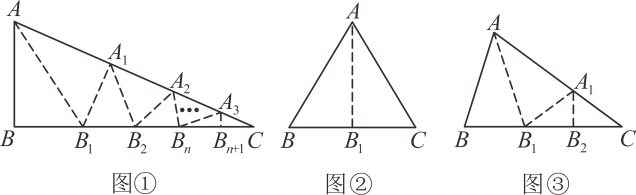
(1) 【问题背景】小强在学习完平行线一节后，想利用平行线的知识证明“三角形的内角和是180°”；．如图1，是小强为证明三角形内角和是180°所采取的构图方法：过△ABC的顶点A作EF∥BC ．

请完成：利用小强的构图，说明∠BAC+∠B+∠C＝180°的理由；

(2) 【尝试应用】如图2，直线l₁与直线l₂相交于点O ，夹角为α，点B在点O右侧，点C在l₁上方，点A在O点左侧运动，点E在射线CO上运动（不与C ， O重合）；

请完成：当α＝60°时，AG平分∠EAB ， EF平分∠AEC交直线AG于点G ，求∠AGE的度数；

(3) 【拓展创新】如图3，点E在线段CO上运动（不与C ， O重合），∠AEF＝n∠AEC ， ∠EAG＝m∠EAB ， m+2n＝1，EF交AG于点G；

请完成：当n为何值时，∠AGE不随∠EAB的变化而变化，并用含α的代数式表示∠AGE的度数（写出解答过程）．

【考点】

三角形内角和定理; 三角形的外角性质; 角平分线的概念;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 【探究】如图①， $\text{[math]}$ 和 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ， $\text{[math]}$ 经过点 $\text{[math]}$ 且平行于 $\text{[math]}$ ，分别与 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ．

（1）若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 　　度， $\text{[math]}$ 　　度．

（2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

【拓展】如图②， $\text{[math]}$ 和 $\text{[math]}$ 的平分线交于点 $\text{[math]}$ ， $\text{[math]}$ 经过点 $\text{[math]}$ 且平行于 $\text{[math]}$ ，分别与 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ．若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的度数．（用含 $\text{[math]}$ 的代数式表示）

实践探究题普通

2. 在锐角 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 的顶点 $\text{[math]}$ 放置在 $\text{[math]}$ 边上，使 $\text{[math]}$ 的两边分别与边 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ 不与 $\text{[math]}$ 点重合，点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合）.设 $\text{[math]}$ ， $\text{[math]}$ .

(1) 【发现】

若 $\text{[math]}$ .

如图1，当点 $\text{[math]}$ 与点 $\text{[math]}$ 重合， $\text{[math]}$ 时， $\text{[math]}$ °；

如图2，当点 $\text{[math]}$ ， $\text{[math]}$ 均不与点 $\text{[math]}$ 重合时， $\text{[math]}$ °

图1 图2

(2) 【探究】

判断 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 之间满足怎样的数量关系？并写出你的理由.

实践探究题困难

3. 如图①，在△ABC中，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，剪掉重复部分……将余下部分沿∠B_nA_nC的平分线A_nB_n+1折叠，点B_n与点C重合，无论折叠多少次，只要最后一次恰好重合，则称∠BAC是△ABC的好玩角．

小马展示了确定∠BAC是△ABC的好玩角的两种情形．

情形一：如图②，沿等腰三角形ABC顶角∠BAC的平分线AB₁折叠，点B与点C重合；

情形二：如图③，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，此时点B₁与点C重合．

(1) 探究发现：

在△ABC中，∠B=66°，∠B>∠C，经过两次折叠，∠BAC是△ABC的好玩角，求∠C的度数．

(2) 小马经过三次折叠发现了∠BAC是△ABC的好玩角，请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系为．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好玩角，则∠B与∠C(不妨设∠B>∠C)之间的等量关系为．

(3) 应用提升：

小马找到一个三角形，三个角分别为20°，60°，100°，发现60°和100的两个角都是此三角形的好玩角．请你完成，如果一个三角形的最小角是18°试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好玩角．

实践探究题困难