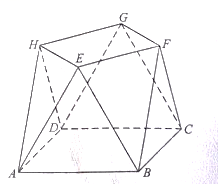
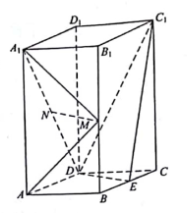
如图1，、、分别是边长为4的正方形的三边、、的中点，先沿着虚线段将等腰直角三角形裁掉，再将剩下的五边形沿着线段折起，连接、就得到了一个空间五面体，如图2．

1. 如图1， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别是边长为4的正方形的三边 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点，先沿着虚线段 $\text{[math]}$ 将等腰直角三角形 $\text{[math]}$ 裁掉，再将剩下的五边形 $\text{[math]}$ 沿着线段 $\text{[math]}$ 折起，连接 $\text{[math]}$ 、 $\text{[math]}$ 就得到了一个空间五面体，如图2．

(1) 若 $\text{[math]}$ 是四边形 $\text{[math]}$ 对角线的交点，求证： $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求三棱锥 $\text{[math]}$ 的体积．

【考点】

棱柱、棱锥、棱台的体积; 直线与平面平行的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 已知球内接正四棱锥 $\text{[math]}$ 的高为 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 相交于 $\text{[math]}$ ，球的表面积为 $\text{[math]}$ ，若 $\text{[math]}$ 为 $\text{[math]}$ 中点.

(1) 求证： $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 求三棱锥 $\text{[math]}$ 的体积.

解答题普通

2. 如图，在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ $\text{[math]}$ ，平面 $\text{[math]}$ 平面 $\text{[math]}$ ，平面 $\text{[math]}$ 平面 $\text{[math]}$ .

(1) 点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，求证： $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求三棱锥 $\text{[math]}$ 体积的最大值.

解答题普通

3. 如图，四棱锥 $\text{[math]}$ 中，底面ABCD为直角梯形. $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为等边三角形，平面 $\text{[math]}$ 平面ABCD.

(1) 若M为PB的中点，证明： $\text{[math]}$ 面PAD；

(2) 求三棱锥 $\text{[math]}$ 的体积.

解答题普通