1.
如图,已知菱形 的边长为
的边长为 ,
,  , 点
, 点 、
、 分别是边
分别是边 、
、 上的两个动点,
上的两个动点, , 连接
, 连接 .
.
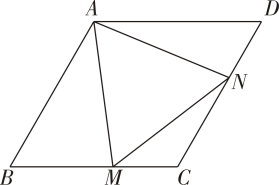
(1)
 是等边三角形吗?如是,请证明;如不是,请说明理由.
(2)
在
是等边三角形吗?如是,请证明;如不是,请说明理由.
(2)
在 、
、 运动的过程中,
运动的过程中, 的面积存在最大值吗?如存在,请求出该最大值;如不存在,请说明理由.
的面积存在最大值吗?如存在,请求出该最大值;如不存在,请说明理由.
【考点】
等边三角形的判定与性质;
菱形的性质;