1.
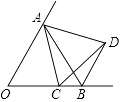
如图,在 中,
中, ,
,  ,
,  . 动点P从点A出发,沿着A→C→B→A的路径,以每秒
. 动点P从点A出发,沿着A→C→B→A的路径,以每秒 的速度运动,当P回到A点时运动结束,设点P运动的时间为t秒.
的速度运动,当P回到A点时运动结束,设点P运动的时间为t秒.

(1)
当 时,求
时,求 的面积;
(2)
若
的面积;
(2)
若 平分
平分 , 求t的值;
(3)
深入探索:若点P运动到边
, 求t的值;
(3)
深入探索:若点P运动到边 , 且
, 且 是等腰三角形,求t的值.
是等腰三角形,求t的值.
【考点】
三角形-动点问题;
能力提升
真题演练