1.
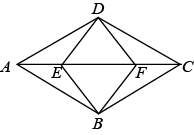
如图,已知在菱形 中,
中, ,
,  , 对角线
, 对角线 与
与 交于点O,点E是射线
交于点O,点E是射线 上的一个动点,将线段
上的一个动点,将线段 绕点D顺时针旋转
绕点D顺时针旋转 得到线段
得到线段 , 连结
, 连结 ,
,  ,
,  .
.

(1)
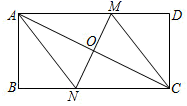
如图1,当点E在线段 上运动时,
(2)
在点E的整个运动过程中,将
上运动时,
(2)
在点E的整个运动过程中,将 沿着DE翻折得到四边形
沿着DE翻折得到四边形 , 当四边形
, 当四边形 为菱形时,求出此时
为菱形时,求出此时 的面积.
的面积.
①求证:;
②当时,判断四边形
的形状,并说明理由.
【考点】
平行四边形的判定;
菱形的判定与性质;