1.
如图

(1)
【探究发现】
(2)
【类比迁移】
(3)
【拓展提升】
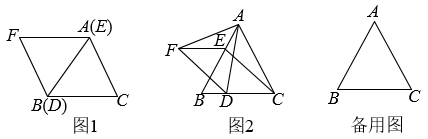
如图1,在中,
.
, 垂足为
, 点
在
上,连接
,
. 则有下列命题:①
;②
, 请你从中选择一个命题证明其真假,并写出证明过程.
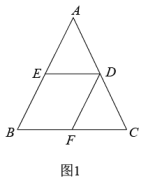
如图2,在中,
,
, 点
在三角形的内部,过点
作
, 且
, 连接
. 求证:
.
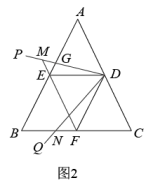
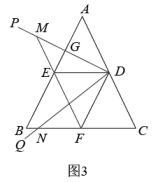
如图3.在中,
,
, 把线段
绕点
顺时针方向旋转
到
, 把线段
绕点
逆时针旋转
到
, 分别连接
,
,
, 请直接写出
面积的最大值.
【考点】
三角形的综合;
能力提升
真题演练