1.
如图, 中,点D、E分别为
中,点D、E分别为 的中点,延长
的中点,延长 到点F,使得
到点F,使得 , 连接
, 连接 . 求证:
. 求证:
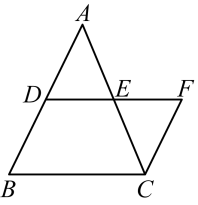
(1)
 ;
(2)
四边形
;
(2)
四边形 是平行四边形.
是平行四边形.
【考点】
平行四边形的判定;
三角形全等的判定-SAS;
三角形的中位线定理;




