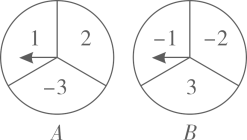
甲、乙两人用如图所示的两个转盘做游戏，转盘被等分为三份，分别标有数字1，2，-3；转盘也被等分成三份，分别标有数字-1，-2，3．甲乙两人同时转动转盘，当转盘停止转动时，记下两个转盘指针所指的数字之和．若指针所指数字之和为正数，则甲胜；指针所指数字之和为负数，则乙胜．

1. 甲、乙两人用如图所示的两个转盘做游戏， $\text{[math]}$ 转盘被等分为三份，分别标有数字1，2，-3； $\text{[math]}$ 转盘也被等分成三份，分别标有数字-1，-2，3．甲乙两人同时转动转盘，当转盘停止转动时，记下两个转盘指针所指的数字之和．若指针所指数字之和为正数，则甲胜；指针所指数字之和为负数，则乙胜．

(1) 转动 $\text{[math]}$ 转盘一次，指针所指数字为负数的概率是；

(2) 请用列表或画树状图的方法说明这个游戏对甲乙两人是否公平．

【考点】

用列表法或树状图法求概率; 游戏公平性; 概率公式;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 甲、乙两人做游戏，他们在一只不透明的袋子中装了五个小球，分别标有数字：1，1，2，2，3，这些小球除编号外都相同．

(1) 搅匀后，甲从中任意摸出一个小球，则这个小球的编号是偶数的概率为；

(2) 搅匀后，甲从中任意摸出一个小球，记录小球的编号后放回、搅匀，乙再从中任意摸出一个小球，若摸出两个小球编号之和为偶数甲获胜；否则，乙获胜，请你用画树状图或列表的方法说明谁获胜的概率大．

综合题普通

2. 如图，有4张分别印有Q版西游图案的卡片：A唐僧、B孙悟空、C猪八戒、D沙悟净.

现将这4张卡片（卡片的形状、大小，质地都相同）放在不透明的盒子中，搅匀后从中任意取出1张卡片，记录后放回、搅匀，再从中任意取出1张卡片.求下列事件发生的概率：

(1) 第一次取出的卡片图案为“B孙悟空”的概率为；

(2) 用画树状图或列表的方法，求两次取出的2张卡片中至少有1张图案为“A唐僧”的概率.

综合题普通

3. 勾股定理是人类早期发现并证明的重要数学定理之一，至今已有几百种证明方法，在中国，商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释并创制了一幅“勾股圆方图”；后刘徽用“出入相补”原理证明了勾股定理；清朝末年，数学家华蘅芳提出了二十多种对于勾股定理证法．

(1) 某学校数学活动室进行文化建设，拟从以上4位科学家的画像中随机选用1幅，恰好选中的画像是刘徽的概率；

(2) 在某次数学活动中，有一个不透明的信封内装有三根长度分别为4cm，6cm和8cm的细木棒，木棒露出纸袋外的部分长度相等，小亮手中有一根长度为 $\text{[math]}$ cm的细木棒，现从信封内随机取出两根细木棒与小亮手中的细木棒首尾相接放在一起，求抽出的细木棒能与小亮手中的细木棒构成直角三角形的概率（用画树状图或列表的方法求解）

综合题普通