1.
实践与探究
(1)
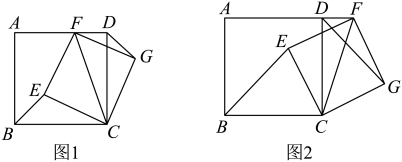
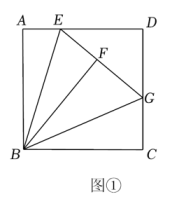
操作一:如图①,对折矩形纸片 , 使
, 使 与
与 重合,折痕为
重合,折痕为 . 把纸片展平后,将矩形纸片
. 把纸片展平后,将矩形纸片 沿过点D的直线折叠,使点A落在
沿过点D的直线折叠,使点A落在 上,点A的对应点为点
上,点A的对应点为点 , 折痕为
, 折痕为 , 连结
, 连结 .
(2)
操作二:如图②,在矩形
.
(2)
操作二:如图②,在矩形 中,
中, ,
,  . 先将矩形纸片
. 先将矩形纸片 沿过点D的直线折叠,使点A落在矩形
沿过点D的直线折叠,使点A落在矩形 的内部,点A的对应点为点
的内部,点A的对应点为点 , 折痕为
, 折痕为 . 然后沿过点D的直线折叠,使点C落在直线
. 然后沿过点D的直线折叠,使点C落在直线 上,折痕为
上,折痕为 , 点C的对应点为点
, 点C的对应点为点 . 再将矩形沿过点G的直线继续折叠,折痕为
. 再将矩形沿过点G的直线继续折叠,折痕为 , 点B的对应点为点
, 点B的对应点为点 . 我们发现,点H的位置不同,点B的位置也不同.当点
. 我们发现,点H的位置不同,点B的位置也不同.当点 恰好与点
恰好与点 . 重合时,线段
. 重合时,线段 的长为.
的长为.

①当矩形是正方形时,
是 ▲ 三角形;
②当是等腰直角三角形时,求边
与边
之间的数量关系;
③若点P、、C共线,求证:
.

【考点】
正方形的性质;
四边形的综合;