1.
综合运用.
(1)
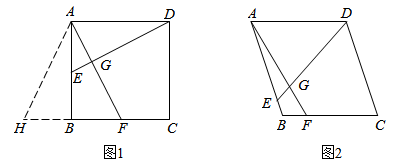
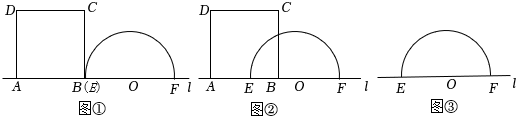
如图( ),已知:在
),已知:在 中,
中, ,
,  , 直线
, 直线 经过点
经过点 ,
,  ,
,  , 垂足分别为点
, 垂足分别为点 ,
,  . 证明:
. 证明: .
(2)
如图(
.
(2)
如图( ),将(
),将( )中的条件改为:在
)中的条件改为:在 中,
中, ,
,  ,
,  ,
,  三点都在直线
三点都在直线 上,并且有
上,并且有 , 其中
, 其中 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论 是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)
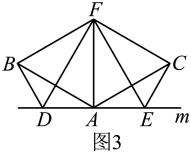
拓展与应用:如图(
是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)
拓展与应用:如图( ),
), ,
,  是
是 ,
,  ,
,  三点所在直线
三点所在直线 上的两动点(
上的两动点( ,
,  ,
,  三点互不重合),点
三点互不重合),点 为
为 平分线上的一点,且
平分线上的一点,且 和
和 均为等边三角形,连接
均为等边三角形,连接 ,
,  , 若
, 若 , 试判断
, 试判断 的形状并说明理由.
的形状并说明理由.


【考点】
三角形全等的判定;
等边三角形的判定与性质;