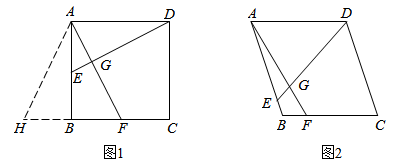
问题解决：如图1，在矩形中，点分别在边上，于点 .

1. 问题解决：如图1，在矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别在 $\text{[math]}$ 边上， $\text{[math]}$ 于点 $\text{[math]}$ .

(1) 求证：四边形 $\text{[math]}$ 是正方形；

(2) 延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$ ，判断 $\text{[math]}$ 的形状，并说明理由.

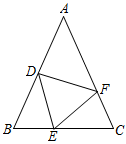
类比迁移：如图2，在菱形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别在 $\text{[math]}$ 边上， $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

【考点】

三角形全等的判定; 等腰三角形的判定与性质; 等边三角形的判定与性质; 矩形的性质; 正方形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 综合运用．

(1) 如图（ $\text{[math]}$ ），已知：在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点 $\text{[math]}$ ， $\text{[math]}$ ．证明： $\text{[math]}$ ．

(2) 如图（ $\text{[math]}$ ），将（ $\text{[math]}$ ）中的条件改为：在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点都在直线 $\text{[math]}$ 上，并且有 $\text{[math]}$ ，其中 $\text{[math]}$ 为任意锐角或钝角．请问结论 $\text{[math]}$ 是否成立？如成立，请你给出证明；若不成立，请说明理由．

(3) 拓展与应用：如图（ $\text{[math]}$ ）， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点所在直线 $\text{[math]}$ 上的两动点（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点互不重合），点 $\text{[math]}$ 为 $\text{[math]}$ 平分线上的一点，且 $\text{[math]}$ 和 $\text{[math]}$ 均为等边三角形，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，试判断 $\text{[math]}$ 的形状并说明理由．

综合题普通

2. 如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC上，且BE=CF，BD=CE．

(1) 求证：△DEF是等腰三角形；

(2) 当∠A=60°时，求∠EDF的度数；

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D在 $\text{[math]}$ 内， $\text{[math]}$ ， $\text{[math]}$ ，点E在 $\text{[math]}$ 外， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 判断 $\text{[math]}$ 的形状并加以证明．

(2) 连接DE，若 $\text{[math]}$ ， $\text{[math]}$ ，求DE的长．

综合题普通