1.
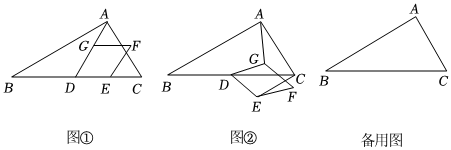
如图,已知菱形ABCD, E为对角线AC上一点.

(1)
[建立模型]
如图1,连结BE, DE.求证:∠EBC=∠EDC.
(2)
[模型应用]
如图2, F是DE延长线上一点,∠EBF=∠ABC, EF交AB于点G.
(3)
[模型迁移]
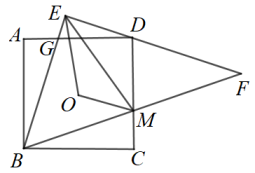
F是DE延长线上一点,∠EBF=∠ABC, EF交射线AB于点G,且sin∠BAC= , BF//AC.求
, BF//AC.求 的值.
的值.
如图1,连结BE, DE.求证:∠EBC=∠EDC.
如图2, F是DE延长线上一点,∠EBF=∠ABC, EF交AB于点G.
①判断△FBG的形状,并说明理由.
②若G为AB的中点,且AB=4,∠ABC=60°, 求AF的长.
F是DE延长线上一点,∠EBF=∠ABC, EF交射线AB于点G,且sin∠BAC=
【考点】
解直角三角形;
四边形的综合;
能力提升
真题演练