1.
一个四棱台的三视图如图所示,其中正视图和侧视图均为上底长为2,下底长为4,腰长为2的等腰梯形,则该四棱台的体积为( )
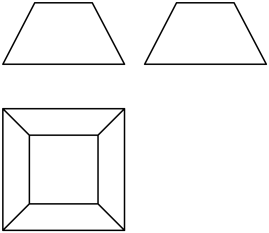
A.
 B.
B.
 C.
C.
 D.
56
D.
56
【考点】
组合几何体的面积、表面积、体积问题;