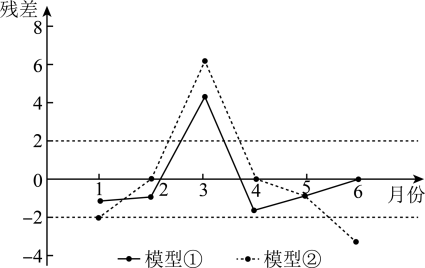
某互联网公司为了确定下一季度的前期广告投入计划，收集了近个月广告投入量（单位：万元）和收益（单位：万元）的数据如下表：月份广告投入量收益他们分别用两种模型① ， ②分别进行拟合，得到相应的回归方程并进行残差分析，得到如下图所示的残差图及一些统计量的值．附：回归方程中斜率和截距的最小二乘估计公式分别为：，．

1. 某互联网公司为了确定下一季度的前期广告投入计划，收集了近 $\text{[math]}$ 个月广告投入量 $\text{[math]}$ （单位：万元）和收益（单位：万元）的数据如下表：

月份	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
广告投入量	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
收益	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

他们分别用两种模型① $\text{[math]}$ ， ② $\text{[math]}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如下图所示的残差图及一些统计量的值．

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

附：回归方程 $\text{[math]}$ 中斜率和截距的最小二乘估计公式分别为： $\text{[math]}$ ， $\text{[math]}$ ．

(1) 根据残差图，比较模型①②的拟合效果，应该选择哪个模型？请说明理由．

(2) 残差绝对值大于 $\text{[math]}$ 的数据认为是异常数据，需要剔除．

（i）剔除异常数据后求出（1）中所选模型的回归方程；

（ii）若广告投入量 $\text{[math]}$ ，求该模型收益的预报值是多少？

【考点】

线性回归方程;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 2024年2月10日至17日（正月初一至初八），“2024·内江市中区新春极光焰火草地狂欢节”在川南大草原举行，共举行了8场精彩的烟花秀节目．前5场的观众人数（单位：万人）与场次的统计数据如表所示：

场次编号x	1	2	3	4	5
观众人数y	$\text{[math]}$	$\text{[math]}$	1	$\text{[math]}$	$\text{[math]}$

参考公式及参考数据：回归方程 $\text{[math]}$ 中斜率与截距的最小二乘法估计公式分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，其中 $\text{[math]}$ ．

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
k	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

(1) 已知可用线性回归模型拟合y与x的关系，请建立y关于x的线性回归方程；

(2) 若该烟花秀节目分A、B、C三个等次的票价，某机构随机调查了该烟花秀节目现场200位观众的性别与购票情况，得到的部分数据如表所示，请将2×2列联表补充完整，并判断能否有90%的把握认为该烟花秀节目的观众是否购买A等票与性别有关．

	购买A等票	购买非A等票	总计
男性观众		50
女性观众	60
总计		100	200

解答题普通

2. 2016～2020年广西城乡居民人均可支配收入的柱形图如下图所示．

参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

附：样本的相关系数 $\text{[math]}$ ，

线性回归方程 $\text{[math]}$ 中的系数 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 不考虑价格因素，求广西2020年农村居民人均可支配收入的年增长率（结果精确到0.1%）．

(2) 现欲了解广西各年城镇居民人均可支配收入y（单位：元）与农村居民人均可支配收入x（单位：元）是否存在较好的线性关系．设广西2016年城镇居民人均可支配收入为 $\text{[math]}$ 元，农村居民人均可支配收入为 $\text{[math]}$ 元，2017年对应的数据分别为 $\text{[math]}$ ， $\text{[math]}$ ， 2018年对应的数据分别为 $\text{[math]}$ ， $\text{[math]}$ ， 2019年对应的数据分别为 $\text{[math]}$ ， $\text{[math]}$ ， 2020年对应的数据分别为 $\text{[math]}$ ， $\text{[math]}$ ．根据图中的五组数据，得到y关于x的线性回归方程为 $\text{[math]}$ ．试问y关于x的线性相关系数r是否大于0.95，并判断y与x之间是否存在较好的线性关系．

解答题普通

3. $\text{[math]}$ ， $\text{[math]}$ 是河道分布密集、水患严重的西部两邻县．从2015年开始，沿海 $\text{[math]}$ 市对 $\text{[math]}$ 县对口整治河道． $\text{[math]}$ 市2015年对 $\text{[math]}$ 县河道整治投入40亿元，以后河道整治投入逐年减少 $\text{[math]}$ 亿元（ $\text{[math]}$ 是常数， $\text{[math]}$ ． $\text{[math]}$ 县则由当地市级机关下派第一书记，单位承包到镇（乡）河道，实行河长负责，市民承包到河段的责任制．如表是从2015年到2019年，对 $\text{[math]}$ 县以每年为单位的河道整治投入额：

投入年份	2015	2016	2017	2018	2019
年分代号t	1	2	3	4	5
年河道整治投入额y（亿元）	30	24	22	18	16

参考公式及数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ ．

(1) 用最小二乘法求对 $\text{[math]}$ 县的河道整治投入额 $\text{[math]}$ 与投入年份代号 $\text{[math]}$ 的回归方程；

(2) $\text{[math]}$ ， $\text{[math]}$ 两县人口分别为58万和42万，请比较对 $\text{[math]}$ ， $\text{[math]}$ 两县从2015年至2020年这6年人均河道整治投入的大小（对 $\text{[math]}$ 县2020年的河道整治投入取回归方程的估计值）

解答题普通