1.
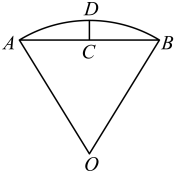
《几何原本》是古希腊数学家欧几里得的一部不朽之作,书中称轴截面为等腰直角三角形的圆锥为直角圆锥,则直角圆锥侧面展开图的圆心角的弧度数为( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
扇形的弧长与面积;