1.
(1)
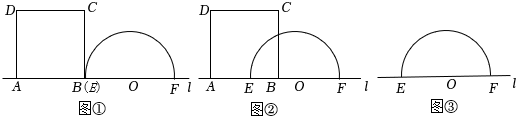
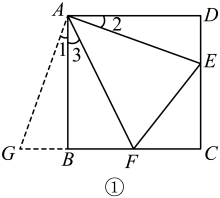
方法探索:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.(根据所给的铺助线完成证明)
(2)
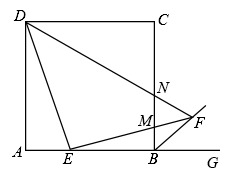
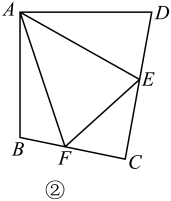
方法拓展:如图②.在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF= ∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.并证明你的猜想.
(3)
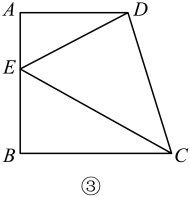
知识应用:如图③,在四边形ABCD中,∠A=∠B=90°,AB=BC=5,AD=4,E是边AB上一点,且∠DCE=45°,求AE的长度.
∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.并证明你的猜想.
(3)
知识应用:如图③,在四边形ABCD中,∠A=∠B=90°,AB=BC=5,AD=4,E是边AB上一点,且∠DCE=45°,求AE的长度.
【考点】
三角形全等的判定;
勾股定理;
正方形的性质;
能力提升
真题演练