1.
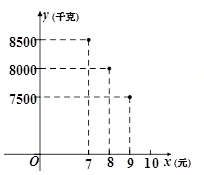
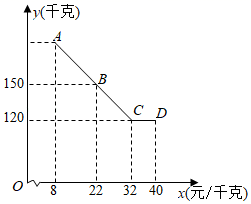
自2020年3月开始,我国生猪、猪肉价格持续上涨,某大型菜场在销售过程中发现,从2020年10月1日起到11月9日的40天内,猪肉的每千克售价与上市时间的关系用图1的一条折线表示:猪肉的进价与上市时间的关系用图2的一段抛物线 表示.
表示.

(1)
 ;
(2)
求图1表示的售价
;
(2)
求图1表示的售价 与时间
与时间 的函数关系式;
(3)
问从10月1日起到11月9日的40天内第几天每千克猪肉利润最低,最低利润为多少?
的函数关系式;
(3)
问从10月1日起到11月9日的40天内第几天每千克猪肉利润最低,最低利润为多少?
【考点】
二次函数与一次函数的综合应用;
二次函数的实际应用-销售问题;
能力提升
真题演练