如图，等腰直角三角形ABC中，∠BAC＝90°，D、E分别为AB、AC边上的点，AD＝AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．

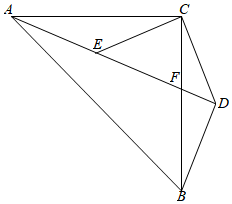
1. 如图，等腰直角三角形ABC中，∠BAC＝90°，D、E分别为AB、AC边上的点，AD＝AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．

(1) 求证：△ADC≌△AEB；

(2) 判断△EGM是什么三角形，并证明你的结论；

(3) 判断线段BG、AF与FG的数量关系并证明你的结论．

【考点】

等腰三角形的判定与性质; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知：如图，△ABC和△CDE均为等腰三角形，AC＝BC，EC＝DC，BD⊥AD于点D，AD交BC于点F，点A、E、D三点共线，连接BD.

(1) 若∠ACE＝∠BCD，AD＝8，BD＝ $\text{[math]}$ AD，求DE的长；

(2) 若∠ACB＝∠ECD＝90°，且BD＝CE，求证：BC＝AB﹣CF.

综合题普通

2. 如图，阳阳为了测量楼高 $\text{[math]}$ ，在旗杆 $\text{[math]}$ 与楼之间选定一点 $\text{[math]}$ ，使 $\text{[math]}$ ，量得点 $\text{[math]}$ 到楼底距离 $\text{[math]}$ 与旗杆高度 $\text{[math]}$ 都为 $\text{[math]}$ ，旗杆与楼之间的距离 $\text{[math]}$ ，求楼高 $\text{[math]}$ ．

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边的中点，过点A作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ，且 $\text{[math]}$ ．求证：

(1) $\text{[math]}$ $\text{[math]}$ ；

(2) $\text{[math]}$ ．

综合题困难