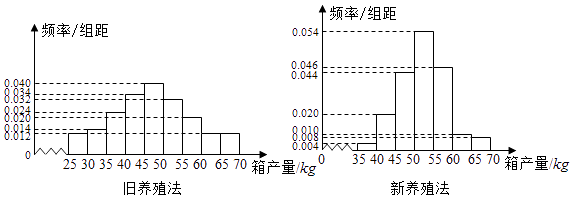
因疫情防控需要，某社区每天都要在上午6点到8点之间对全社区居民完成核酸采集，该社区有两个居民小区，两小区的居住人数之比为9：11，这两个小区各设有一个核酸采集点，为了解该社区居民的核酸采集排队时间，用按比例分配分层随机抽样的方法在两小区中随机抽取了100位居民，调查了他们一次核酸采集排队时间，根据调查结果绘制了如下频率分布直方图．

0 返回首页

1. 因疫情防控需要，某社区每天都要在上午6点到8点之间对全社区居民完成核酸采集，该社区有 $\text{[math]}$ 两个居民小区，两小区的居住人数之比为9：11，这两个小区各设有一个核酸采集点，为了解该社区居民的核酸采集排队时间，用按比例分配分层随机抽样的方法在两小区中随机抽取了100位居民，调查了他们一次核酸采集排队时间，根据调查结果绘制了如下频率分布直方图．

(1) 由直方图分别估计该社区居民核酸采集排队时间的平均时长和在一次核酸采集中排队时长超过16分钟的居民比例；

(2) 另据调查，这100人中一次核酸采集排队时间超过16分钟的人中有20人来自 $\text{[math]}$ 小区，根据所给数据，填写完成下面 $\text{[math]}$ 列联表，并依据小概率值 $\text{[math]}$ 的独立性检验，能否认为排队时间是否超过16分钟与小区有关联？

	排队时间超过16分钟	排队时间不超过16分钟	合计
A小区
B小区
合计

附表：

$\text{[math]}$	0.100	0.05	0.01	0.005	0.001
$\text{[math]}$	2.706	3.841	6.635	7.879	10.828

附： $\text{[math]}$ ，其中 $\text{[math]}$ ．

参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

【考点】

频率分布直方图; 独立性检验;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 为了解某单位员工的月工资水平，从该单位500位员工中随机抽取了50位进行调查，得到如下频数分布表：

月工资 $\text{[math]}$ 百元	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
男员工数	1	8	10	6	4	4
女员工数	4	2	5	4	1	1