如图，在△ABC中，∠BCA=90°，BC=8，AC=6，点D是AB边上的中点，点E是BC边上的一个动点，连接DE，将△BDE沿DE翻折得到△FDE．

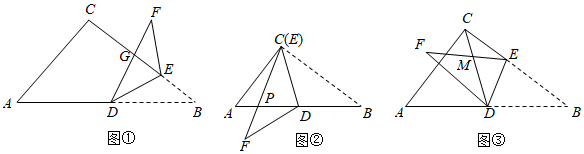
1. 如图，在△ABC中，∠BCA=90°，BC=8，AC=6，点D是AB边上的中点，点E是BC边上的一个动点，连接DE，将△BDE沿DE翻折得到△FDE．

(1) 如图①，线段DF与线段BC相交于点G，当BE=2时，则 $\text{[math]}$ ；

(2) 如图②，当点E与点C重合时，线段EF与线段AB相交于点P，求DP的长；

(3) 如图③，连接CD，线段EF与线段CD相交于点M，当△DFM为直角三角形时，求BE的长．

【考点】

勾股定理; 翻折变换（折叠问题）; 相似三角形的判定与性质; 直角三角形的性质; 直角三角形斜边上的中线;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，△ABC中，∠ACB=90°，AC=3，BC=4．动点P从点A出发，以每秒1个单位长度的速度沿AB向点B运动，连结PC，将△ACP沿PC翻折得到△A'CP，设点P的运动时间为t秒．

(1) 边AB的长为

(2) 用含t的代数式表示线段PC的长．

(3) 当点A'落在△ABC内部(不包括边界)时，求t的取值范围．

(4) 当∠A'CB=∠B时，直接写出t的值．

综合题困难

2. 如图所示，在Rt△ABC中，∠B=90°，AB=6cm，CB=3cm，点P在AC上以 $\text{[math]}$ cm/s的速度从点A匀速运动至点C停止，点Q沿BA方向以2cm/s的速度运动，当点P不与点A重合时，连结PQ，以PQ、BQ为邻边作平行四边形PQBM，当P点停止运动时，点Q也随之停止运动，设点P的运动时间为t(s)．

(2) 当四边形PQBM为矩形时，求t的值；

(3) 当△PQM是钝角三角形时，求t的取值范围．

综合题普通

3. 如图，在四边形纸片ABCD中，AB＝BC，AD＝CD，∠A＝∠C＝90°，∠ABC＝150°，将纸片先沿直线BD对折，再将对折后的图形沿从一个顶点出发的直线剪，剪开后的图形打开铺平，若铺平后的图形中有一个面积为2的平行四边形，求CD的长.

综合题困难