在正方体ABCD﹣A1B1C1D1中，E、F分别是BB1、CD的中点．

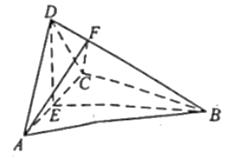
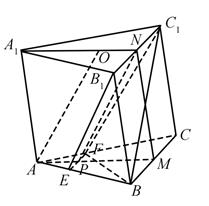
1. 在正方体ABCD﹣A₁B₁C₁D₁中，E、F分别是BB₁、CD的中点．

(1) 求证：平面AED⊥平面A₁FD₁；

(2) 在AE上求一点M，使得A₁M⊥平面ADE．

【考点】

直线与平面垂直的判定; 平面与平面垂直的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，在矩形ABCD中，AB＝2AD ， M为CD的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM.点O是线段AM的中点．求证：

(1) 平面BDO⊥平面ABCM；

解答题普通

2. 如图，矩形 $\text{[math]}$ 和矩形 $\text{[math]}$ 所在的平面与梯形 $\text{[math]}$ 所在的平面分别相交于直线 $\text{[math]}$ 、 $\text{[math]}$ ，其中 $\text{[math]}$ // $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

(1) 证明： $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 求几何体 $\text{[math]}$ 的体积．

解答题普通

3. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，以 $\text{[math]}$ 为折痕将 $\text{[math]}$ 向上折起， $\text{[math]}$ 变为 $\text{[math]}$ ，且平面 $\text{[math]}$ 平面 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 求二面角 $\text{[math]}$ 的大小.

解答题困难