1.
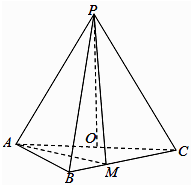
在如图所示的直三棱柱 中,
中, 为正三角形,且
为正三角形,且 , 点
, 点 分别为
分别为 的中点.
的中点.

(1)
求直线 与平面
与平面 所成角的正弦值;
(2)
求二面角
所成角的正弦值;
(2)
求二面角 的余弦值.
的余弦值.
【考点】
直线与平面所成的角;
二面角及二面角的平面角;