1.
矩形ABCD中, =
= (k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.
(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.

(1)
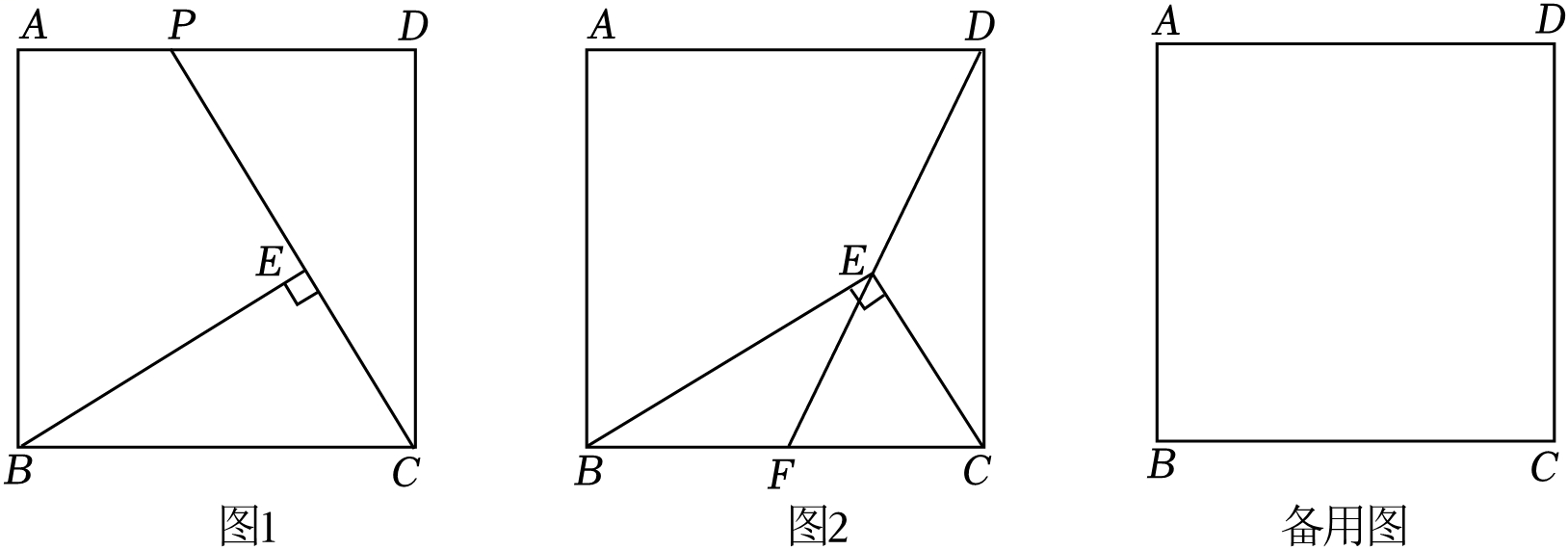
【特例证明】如图(1),当k=2时,求证:AE=EF;
(2)
【类比探究】如图(2),当k≠2时,求 的值(用含k的式子表示);
(3)
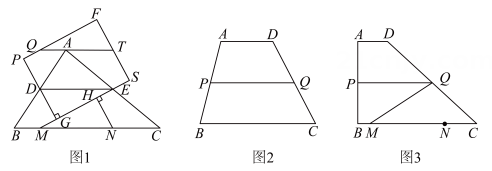
【拓展运用】如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°,
的值(用含k的式子表示);
(3)
【拓展运用】如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°, , 求BC的长.
, 求BC的长.
小明不完整的证明过程如下,请你帮他补充完整.
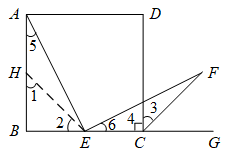
证明:如图,在BA上截取BH=BE,连接EH.
∵k=2, ∴AB=BC. ∵∠B=90°,BH=BE, ∴∠1=∠2=45°, ∴∠AHE=180°-∠1=135°. ∵CF平分∠DCG,∠DCG=90°, ∴∠3= ∴∠ECF=∠3+∠4=135°. ∴…… (只需在答题卡对应区域写出剩余证明过程) |
【考点】
相似三角形的判定与性质;
四边形的综合;
能力提升
真题演练