如图，在Rt△ABC和Rt△EFD中，∠ABC＝∠EFD＝90°，AC＝ED，AC⊥ED，垂足为M，连接AE、CE．

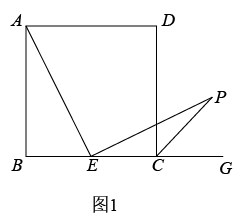
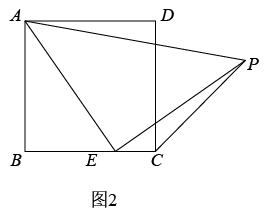
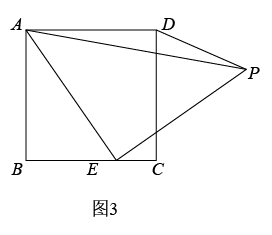
1. 如图，在Rt△ABC和Rt△EFD中，∠ABC＝∠EFD＝90°，AC＝ED，AC⊥ED，垂足为M，连接AE、CE．

(1) △ABC与△EFD全等吗？为什么？

(2) 若∠AEF＝∠DEF，判断∠AEC与∠ACE的数量关系，并说明理由．

【考点】

三角形全等的判定; 等腰三角形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线．

(1) 写出图中全等的三角形，线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的位置关系是；

(2) 如图2，在（1）的条件下，过点B，作 $\text{[math]}$ ，垂足为E，交 $\text{[math]}$ 于点F，且 $\text{[math]}$ ，请说明 $\text{[math]}$ 的理由．

综合题普通

(1) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ 是BC边上一点， $\text{[math]}$ 且 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ .

(2) 如图2，在 $\text{[math]}$ 中， $\text{[math]}$ 是BC边上一点， $\text{[math]}$ ，点 $\text{[math]}$ 在线段AD上且 $\text{[math]}$ $\text{[math]}$ ，求证： $\text{[math]}$ .

(3) 如图3，在 $\text{[math]}$ 中， $\text{[math]}$ 是CB延长线上一点， $\text{[math]}$ ，点 $\text{[math]}$ 在射线DA上且 $\text{[math]}$ $\text{[math]}$ ，请画出 $\text{[math]}$ 点的位置，此时AB和CE满足怎样的数量关系，请说明理由.

综合题普通

3. 如图， $\text{[math]}$ ，垂足分别为D，E，BE与CD相交于点F， $\text{[math]}$

(1) 求证： $\text{[math]}$ ：

(2) 在不添加任何辅助线的前提下，直接写出图中四对全等三角形（注意对应顶点写在对应位置上）。

综合题普通