1.
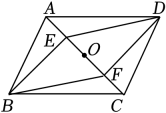
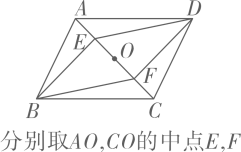
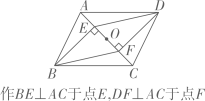
如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别在x轴,y轴的正半轴上,B(2,2),点D在CB边上,E是AB的中点,连接OD,DE,并延长DE交x轴于点P,设CD=m.

(1)
求点P的坐标(用含m的式子表示);
(2)
当OD=PD时,求m的值;
(3)
在第(2)题的条件下,作EF∥x轴交OD于点F,连接CF,
①求证:四边形CDEF是平行四边形;
②四边形CDEF能否为菱形?请说明理由.
【考点】
平行线的性质;
平行四边形的判定;
菱形的判定;
正方形的性质;
三角形全等的判定-ASA;