1.
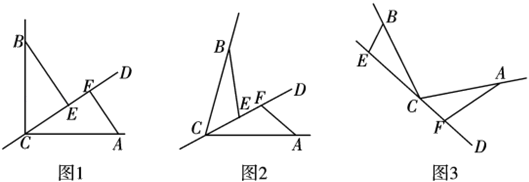
如图,在  和
和  中,
中,  ,
,  ,
,  ,垂足为M,连接EA.
,垂足为M,连接EA.
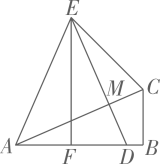
(1)
 与
与  全等吗?为什么?
(2)
若
全等吗?为什么?
(2)
若  ,判断
,判断  与
与  的数量关系,并说明理由.
的数量关系,并说明理由.
【考点】
余角、补角及其性质;
三角形全等的判定-AAS;